
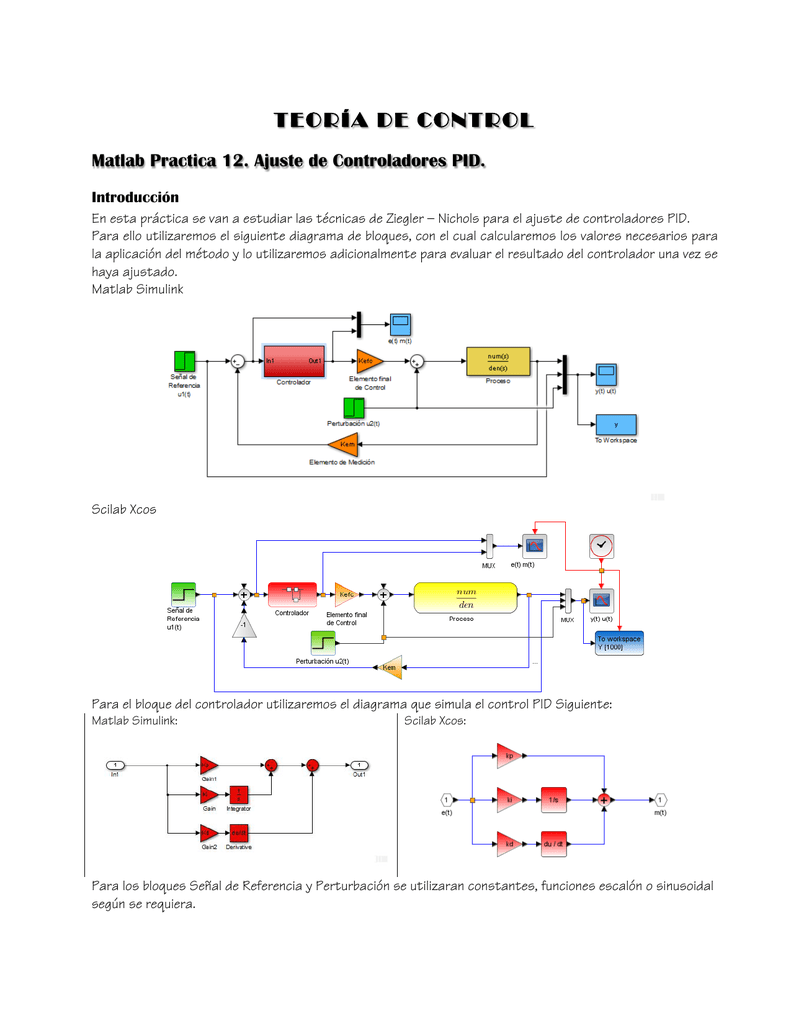
The plant transfer function is a robot joint driven by DC motor model from module 1, with J = 10 and B = 1.įigure 1 pid_feedback.zcos basic PID simulation diagramĬlick on the Simulation Start button to see the step response. It requires only a step_function, clock_c (from Sources palette), PID and CLR blocks (from Continuous time systems palette), SUMMATION (from Mathematical operations palette), MUX (from Signal Routing palette), and CSCOPE (from Sinks palette). This diagram can easily be constructed using Xcos standard palettes. This launches an Xcos diagram in Figure 1.
#Pi in scilab download#
1: To get started with Xcos simulation of a PID feedback system, download file pid_feedback.zcos. Nevertheless, it is easy to convert between parameters of (1) and (4) by the relationsĮx. In this form, the controller gains are distributed to each of the PID terms separately, with its transfer functionįor our discussion of PID controller, we focus on the form (4) and (5). With the transfer function of PID controllerĪnother common structure of PID algorithm is represented by We see that the control variable is a function of 3 terms: P (proportional to error), I (time integral of error), and D (derivative of error), with corresponding control parameters K (proportional gain), T i (integral time), and T d (derivative time), respectively. This algorithm computes the control variable u as output, given the input e, the error between the command and plant output. The so-called “textbook” form of PID controller is described as follows The e-book provides more information on independent robot joint control using PID. For those interested in digital PID implementation, document on this site might be helpful.
#Pi in scilab how to#
So, in this module we discuss some basics of PID control and focus on how to analyze a feedback sysem, with Scilab, build an Xcos diagram and simulate.
Without such knowledge, it could be a frustrating experience to her. Of course, this means the control engineer is certain the plant can be handled by the PID controller and understand how to adjust the control parameters. After some setup and tuning the three PID gains, and perhaps some additional parameters, the system is up and running in no time. Commercial PID controllers can be bought off the shelf and installed in the system. It is a standard control structure used successfully in many industrial applications. PID stands for Proportional, Integral, and Derivative. How to tune PID parameters by Ziegler-Nichols Frequency Domain method.learn how response is degraded by integrator windup.learn the effects of 3 parameters to system response.
Keep practising for different examples and you’ll naturally start to use conditional loops where repetitive calculations are required.įor any questions, observations and queries regarding the article, use the comment form below.This article is contained in Scilab Control Engineering Basics study module, which is used as course material for International Undergraduate Program in Electrical-Mechanical Manufacturing Engineering, Department of Mechanical Engineering, Kasetsart University. Vectorization means that we apply mathematical operations to array (vector) variables instead of scalars (individual elements).įor our particular example we can calculate the f function simply as: ->x = Ĭonditional loops are heavily used in any kind of programming languages.
Vectorization (array programming)įor these simple example we can also use vectorization also named array programming. Using the Scilab function length we extract the number of elements of the vector (in our case is 17). The loop is executed, starting with index 1, for each value of the angle vector. The i is the index of the angle vector, and f is the function we want to calculate. The angle variable is defined as a vector, starting from 0 up to 2π, with π/8 increments. In this example the argument of the function alpha is different than the index i. The Scilab script to evaluate the functions is: angle =


 0 kommentar(er)
0 kommentar(er)
